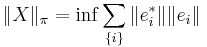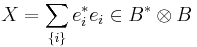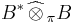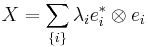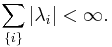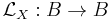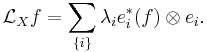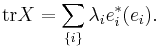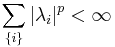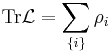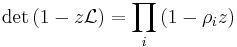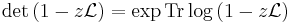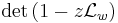Fredholm kernel
In mathematics, a Fredholm kernel is a certain type of a kernel on a Banach space, associated with nuclear operators on the Banach space. They are an abstraction of the idea of the Fredholm integral equation and the Fredholm operator, and are one of the objects of study in Fredholm theory. Fredholm kernels are named in honour of Erik Ivar Fredholm. Much of the abstract theory of Fredholm kernels was developed by Alexander Grothendieck and published in 1955.
Contents |
Definition
Let B be an arbitrary Banach space, and let B* be its dual, that is, the space of bounded linear functionals on B. The tensor product  has a completion under the norm
has a completion under the norm
where the infimum is taken over all finite representations
The completion, under this norm, is often denoted as
and is called the projective topological tensor product. The elements of this space are called Fredholm kernels.
Properties
Every Fredholm kernel has a representation in the form
with 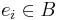 and
and 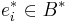 such that
such that 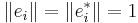 and
and
Associated with each such kernel is a linear operator
which has the canonical representation
Associated with every Fredholm kernel is a trace, defined as
p-summable kernels
A Fredholm kernel is said to be p-summable if
A Fredholm kernel is said to be of order q if q is the infimum of all 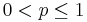 for all p for which it is p-summable.
for all p for which it is p-summable.
Nuclear operators on Banach spaces
An operator 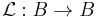 is said to be a nuclear operator if there exists an
is said to be a nuclear operator if there exists an 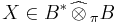 such that
such that 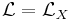 . Such an operator is said to be p-summable and of order q if X is. In general, there may be more than one X associated with such a nuclear operator, and so the trace is not uniquely defined. However, if the order
. Such an operator is said to be p-summable and of order q if X is. In general, there may be more than one X associated with such a nuclear operator, and so the trace is not uniquely defined. However, if the order 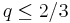 , then there is a unique trace, as given by a theorem of Grothendieck.
, then there is a unique trace, as given by a theorem of Grothendieck.
Grothendieck's theorem
If 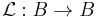 is an operator of order
is an operator of order 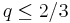 then a trace may be defined, with
then a trace may be defined, with
where 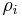 are the eigenvalues of
are the eigenvalues of 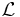 . Furthermore, the Fredholm determinant
. Furthermore, the Fredholm determinant
is an entire function of z. The formula
holds as well. Finally, if 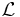 is parameterized by some complex-valued parameter w, that is,
is parameterized by some complex-valued parameter w, that is, 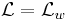 , and the parameterization is holomorphic on some domain, then
, and the parameterization is holomorphic on some domain, then
is holomorphic on the same domain.
Examples
An important example is the Banach space of holomorphic functions over a domain 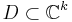 . In this space, every nuclear operator is of order zero, and is thus of trace-class.
. In this space, every nuclear operator is of order zero, and is thus of trace-class.
Nuclear spaces
The idea of a nuclear operator can be adapted to Fréchet spaces. A nuclear space is a Fréchet space where every bounded map of the space to an arbitrary Banach space is nuclear.
References
- Grothendieck A (1955). "Produits tensoriels topologiques et espaces nucléaires". Mem. Am. Math.Soc. 16.
- Grothendieck A (1956). "La théorie de Fredholm". Bull. Soc. Math. France 84: 319–84.
- B.V. Khvedelidze, G.L. Litvinov (2001), "Fredholm kernel", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=f/f041440
- Fréchet M (November 1932). "On the Behavior of the nth Iterate of a Fredholm Kernel as n Becomes Infinite". Proc. Natl. Acad. Sci. U.S.A. 18 (11): 671–3. doi:10.1073/pnas.18.11.671. PMC 1076308. PMID 16577494. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1076308.